今回エンジニアブロクを担当する小瀬です。
経路探索アルゴリズムといえば、A*(エースター)が有名ですが、タワーディフェンスやRTSなど平面的なものに使われる事が多いかと思います。複雑な立体交差などに対応するのは難しいですが、SFC向けに発売されたタクティクスオウガのような地形であれば多少の変更で実現可能です。
A*自体はそれほど難しいものでも無いとは思いますが、基本的な部分としては
- 開始地点から検索を始め、周囲にあるグリッドの移動量とゴールまでの直線距離を求め、その合計をウェイト値として求める。
- 移動先のグリッドからは移動元のグリッドへの方向(または座標)を持たせておく
- ウェイト値計算の行われたグリッドは、探索対象としてリストなどに保持しておく
- リスト中で最もウェイト値の低いグリッドへ移動し、移動元のグリッドはリストから外す
- 隣接グリッドが壁や、既に計算済みのグリッドに囲まれた場合はそのままリストから外す(ただし、計算結果がもとより小さい場合はウェイト値、方向共に上書きする)
- ゴール地点に辿り着くまで上記の流れを繰り返していく。
- 終点に到達したら、そのグリッドの保持する(移動元グリッドへの)方向情報をたどると、始点、終点間の最短距離が導き出せる。
といった機能から成り立っていると言えます。処理的には高速とは言いがたいですが、シンプルでなかなか面白いアルゴリズムだと思います。
文章ではイマイチ説明が難しいのですが、実際のA*時の挙動を分解してみてみると

※本来は1グリッドから4方向に検索する事が多いですが、明らかに遠ざかる方向に関しては省略しています。
S(スタート)から周囲のグリッドを調べ、ステップ数とSからG(ゴール)までの距離を計算します。
この場合では、右側のグリッドのほうがウェイト(f)が低いため、そこからさらに上下に計算を行います。

Sの右上に当たるグリッドが最小値となり、更に上方向へと進めますが、Sの右下のほうが5.60と数値が低いためそちらに切り替えてグリッドを広げます。
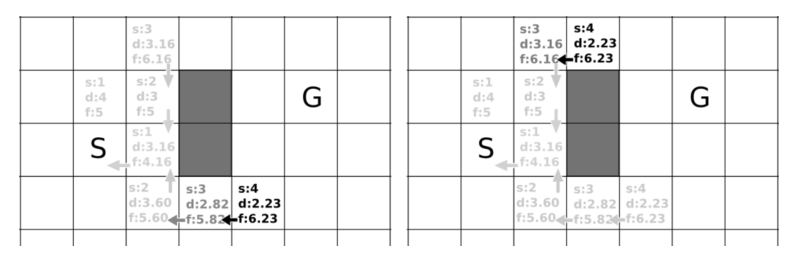

同様にfの値が小さいグリッドに隣接しているグリッドを繰り返し計算していきます。

一部のグリッドが同じウェイト値を持っていますが、どちらを選択しても理論的に移動距離は最短になります。(選択するルートは変化する場合もあります)

いずれかのグリッドがゴールへと繋がり、探索を終了します。各グリッドに割り当てられた矢印を順番に辿って行くと自動的にスタート地点まで繋がっているのがわかるかと思います。
こちらで動画で紹介されているので、動きとしてはイメージしやすいかもしれません。
http://tech.nitoyon.com/ja/blog/2010/01/26/dijkstra-aster-visualize/
これを立体的な地形に対応するには、各グリッドに対し高さ情報を持たせ現在のグリッドと移動先のグリッド高さの差から移動コストを変更するといった方法が考えられます。
以下のコードでは1段登るコストを可変とし、2段以上を壁とみなしています。
private int GridWidth = 30; private int GridHeight = 30; private int GridAltitudeMax = 5; private int UpHillWeight = 1; int[,] Grids; Point startPos; Point goalPos; public void InitGrids() { Grids = new int[GridHeight,GridWidth]; // ランダムからノイズ作成 Random r = new Random(Environment.TickCount); float[,] noise = new float[GridHeight, GridWidth]; for (int y = 0; y < GridHeight; ++y) { for (int x = 0; x < GridWidth; ++x) { noise[x, y] = (float)r.NextDouble(); } } // グリッドの高さを簡易パーリンノイズで初期化 for (int y = 0; y < GridHeight; ++y) { for (int x = 0; x < GridWidth; ++x) { float noise1 = noise[x, y]; float noise2 = cubicInterpolate( noise[x / 2, y / 2], noise[x / 2 + 1, y / 2], noise[x / 2, y / 2 + 1], noise[x / 2 + 1, y / 2 + 1], (float)(x % 2) / 2, (float)(y % 2) / 2); float noise4 = cubicInterpolate( noise[x / 4, y / 4], noise[x / 4 + 1, y / 4], noise[x / 4, y / 4 + 1], noise[x / 4 + 1, y / 4 + 1], (float)(x % 4) / 4, (float)(y % 4) / 4); float pn = noise4 * 0.5f + noise2 * 0.3f + noise1 * 0.2f; Grids[x, y] = (int)((pn - float.Epsilon) * GridAltitudeMax + 1); } } // 始点と終点をランダムでセット startPos.X = r.Next(GridWidth); startPos.Y = r.Next(GridHeight); goalPos.X = r.Next(GridWidth); goalPos.Y = r.Next(GridHeight); DrawGrids(); } protected float cubicInterpolate(float p00, float p01, float p10, float p11, float ix, float iy) { float rx = 1.0f - ix; float ry = 1.0f - iy; float p = (p00 * rx + p01 * ix) * ry + (p10 * rx + p11 * ix) * iy; return p; } struct GridInfo { public Point pos; public float step; public float dist; public float weight; public Point prev; }; GridInfo[,] GridInfos; List<GridInfo> activeGrids = new List<GridInfo>(); public bool SearchPath() { // 全グリッド情報を初期化 GridInfos = new GridInfo[GridWidth,GridHeight]; for (int y = 0; y < GridHeight; ++y) { for (int x = 0; x < GridWidth; ++x) { GridInfos[x, y].pos = new Point(x, y); GridInfos[x, y].step = 0; GridInfos[x, y].dist = 0; GridInfos[x, y].weight = 1e10F; GridInfos[x, y].prev = new Point(0, 0); } } // スタート地点をセット GridInfo info = GridInfos[startPos.X,startPos.Y]; info.dist = calcDist(startPos, goalPos); activeGrids.Clear(); activeGrids.Add(info); while (info.pos != goalPos) { //周囲4グリッドを計算 for (int i = 0; i < 4; ++i) { int sx = ((i % 2 == 0) ? i - 1 : 0); int sy = ((i % 2 == 1) ? i - 2 : 0); int tx = info.pos.X + sx; int ty = info.pos.Y + sy; if (tx < 0 || tx > GridWidth - 1 || ty < 0 || ty > GridHeight - 1) continue; GridInfo neighbor = GridInfos[tx, ty]; // 移動コストを計算。平面のA*であれば通常は 1 で問題なし float weight = calcStepWeight(info.pos, neighbor.pos); if (weight < 0) continue; // 0以下を壁とみなし探索を飛ばす neighbor.step = info.step + weight; neighbor.dist = calcDist(neighbor.pos, goalPos); neighbor.weight = neighbor.step + neighbor.dist; neighbor.prev = info.pos; // 対象のグリッドがすでに計算されていて、ウェイトが低ければ上書きしない if (GridInfos[tx, ty].weight > neighbor.weight) { GridInfos[tx, ty] = neighbor; // ウェイトを元に探索対象リストへ挿入 bool added = false; for (int j = 0; j < activeGrids.Count; ++j) { if (activeGrids[j].weight > neighbor.weight) { activeGrids.Insert(j, neighbor); added = true; System.Diagnostics.Debug.WriteLine("{0},{1},{2}", neighbor.pos.X, neighbor.pos.Y, neighbor.weight); break; } } if (added == false) activeGrids.Add(neighbor); } } //検索済みのグリッドを削除 activeGrids.Remove(info); if (activeGrids.Count() == 0) { // ルートなし return false; } // 次のグリッドをセット info = activeGrids.First(); // 対象がゴール地点なら検索終了 if (goalPos == info.pos) { //GridInfos[tx, ty].prev = info.pos; return true; } } return false; } protected float calcStepWeight(Point p1, Point p2) { // 高さが同一ならば移動コストは通常通り if (Grids[p1.X, p1.Y] == Grids[p2.X, p2.Y]) return 1; // 上り if (Grids[p1.X, p1.Y] < Grids[p2.X, p2.Y]) { int sh = Grids[p2.X, p2.Y] - Grids[p1.X, p1.Y]; if (sh > 2) return -1; // 今回は2段以上を壁とする return 1 + sh * UpHillWeight; // 高さ分コストを加える } // 下り if (Grids[p1.X, p1.Y] > Grids[p2.X, p2.Y]) { int sh = Grids[p1.X, p1.Y] - Grids[p2.X, p2.Y]; if (sh > 2) return -1; // 今回は2段以上を壁とする return 1; // 下りは同一コストとする } return -1; } protected float calcDist(Point p1, Point p2) { float sx = p2.X - p1.X; float sy = p2.Y - p1.Y; return (float)Math.Sqrt(sx * sx + sy * sy); } private void startButton_Click(object sender, EventArgs e) { if (SearchPath()) { Graphics g = pictureBox1.CreateGraphics(); int pixelSize = (pictureBox1.Height > pictureBox1.Width) ? pictureBox1.Width : pictureBox1.Height; float gridW = (float)pixelSize / GridWidth; float gridH = (float)pixelSize / GridHeight; GridInfo info = GridInfos[goalPos.X, goalPos.Y]; Point prevPos = info.pos; DrawGrids(); Pen p = new Pen(Color.Blue); p.Width = 3; do { // グリッド情報をたどり、ゴールからスタートまでラインを引く prevPos = info.pos; info = GridInfos[info.prev.X, info.prev.Y]; g.DrawLine(p, ((float)prevPos.X + 0.5f) * gridW, ((float)prevPos.Y + 0.5f) * gridW, ((float)info.pos.X + 0.5f) * gridW, ((float)info.pos.Y + 0.5f) * gridW); } while (info.pos != startPos); } }
段差のウェイトを1としたもの(左画像)と、ウェイトを10としたもの(右画像)の結果が以下のようになり、段差の移動コストに伴って選択する経路が異なることがわかるかと思います。
上記の例ではパーリンノイズから地形をランダム生成しているため、極端な段差が少なく2段差を壁とみなしましたが、もう少しゲームっぽく考えると、上り方向では2段差を移動量+2とし、3段以上は壁と同じ扱いにする。下り方向に関しては3段までは移動可能とし、4段以上は降りられない。といったような設定をするとそれらしくなるのかなと思います。
3Dが主流となり、グリッドベースのゲームを作る機会が減っているかもしれませんが、シミュレーションゲーム等を作成する際の参考になれば幸いです。

